Approximate Solution Methods

这本书讲的很好，比较系统，适合自学，这里只是我摘录的一些笔记，供自己翻看，内容组织很乱，这本书网上有一些按章节总结的很具体的文章如需要可以搜索，有时间的话建议读原作：）

本书第一部分介绍的是强化学习各种算法基于Tabular Solution Methods场景下的应用，“Tabular Solution Methods”有个问题就是只能处理有限的状态和动作，如果状态或动作个数特别大甚至达到无穷多个，“Tabular Solution Methods”就很难甚至不能求解了，函数近似的核心原理是基于有指导的机器学习，通过与环境的一些交互得到有限的数据，如果模型能够在这些数据上进行比较好的拟合，通过机器学习算法的泛化能力可以认为在未知的环境和状态下也有比较好的预测性能，这一部分里价值函数或者q函数或者policy本身被用函数的形式表达，而基础的RL算法原理并不改变，还是如同第一部分所讲

价值函数拟合

目标函数:

\[ \\ \overline{VE}(w) = \sum_{s \in S} \mu(s) [v_\pi(s) - \widehat{v}(s,w) ]^2\\ \\ \mu(s) = \frac{\eta(s)}{\sum_{s' \in S} \eta(s')} \]

其中\(\eta(s)\)是状态s出现的次数

蒙特卡洛方法学习，优势是收敛性好，但是学习方差比较大，收敛速度慢

TD方法和MC的优劣势相反，不是所有情况都收敛：

TD(n)

动作价值函数拟合

Sarsa

n-step Sarsa

死亡三合音

chapter 11.2给了一个off-policy模型不收敛的例子

以下三合音一起出现就会导致不收敛的问题，如果不是同时出现，可以想办法绕开不收敛问题 + 函数近似 + bootstrapping + off-policy training

Eligibility Traces

\(TD(\lambda)\)可以理解为是对n-step方法的一种融合，对多组n-step进行加权平均

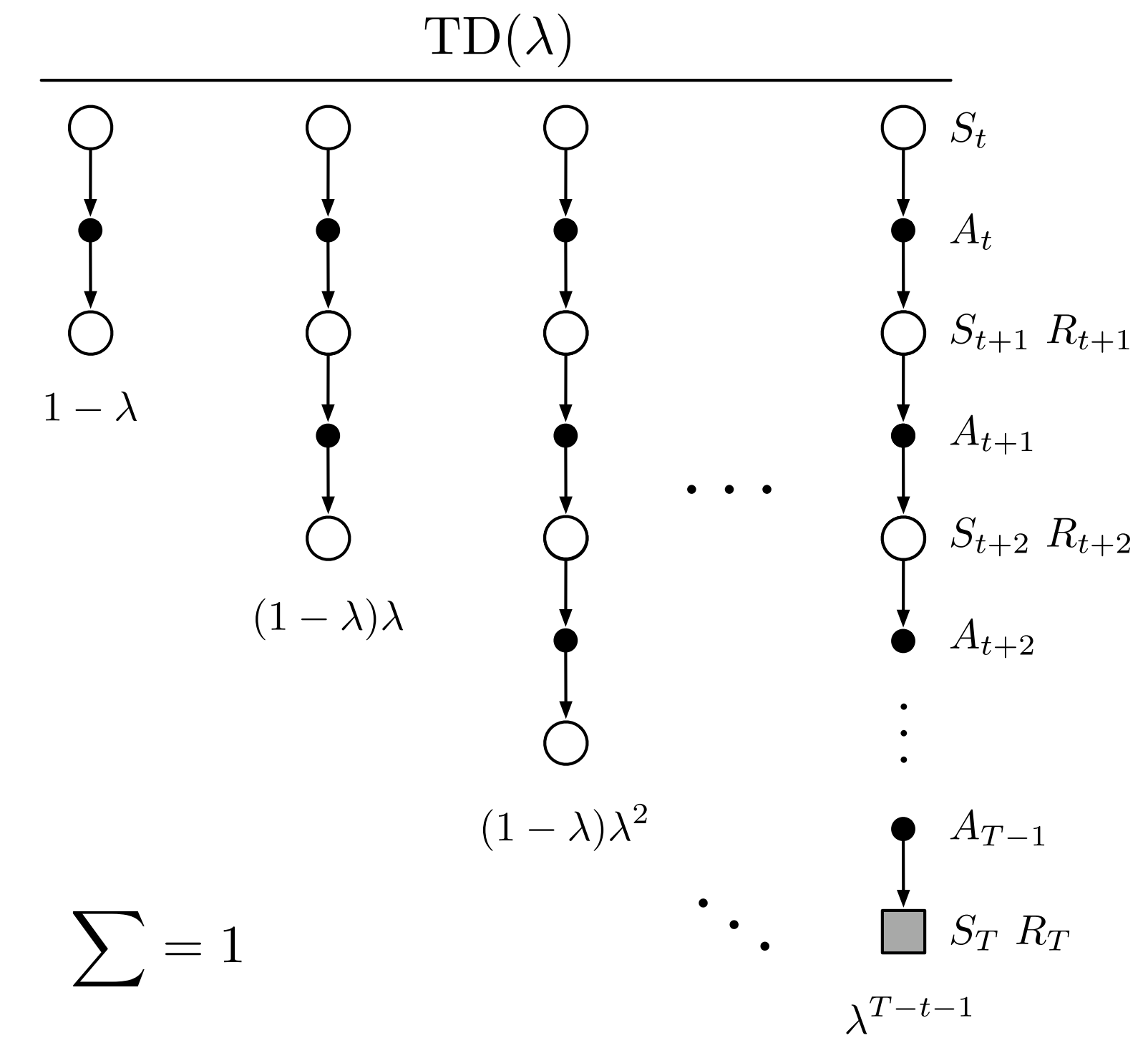
\[ G^\lambda_t = (1-\lambda)\sum_{n=1}^{T-t-1} \lambda^{n-1} G_{t:t+n} + \lambda^{T-t-1} G_t \] \(1-\lambda\)是保证求和为1，当\(\lambda = 1\)时公式退化为MC，\(\lambda=0\)时退化为one-step TD

eligibility trace 形式上有点像优化算法里的冲量

Sarsa(\lambda)

policy gradient method

针对policy建模，这个建模过程中可以把针对策略的先验知识融入进去（注意本书第一部分里面强调不要把先验知识融入到奖励设计中）

policy gradient的收敛性很好

REINFORCE

其中 \[ \bigtriangledown ln \pi (A_t|S_t, \theta_t) = \frac{\bigtriangledown \pi (A_t|S_t, \theta_t) }{ \pi (A_t|S_t, \theta_t)} \]

REINFORCE baseline

带baseline的方法相对于原方法引入了b(s)

\[ \bigtriangledown J( \theta ) \propto \sum_s \mu (s) \sum_a (q_\pi(s, a) - b(s)) \bigtriangledown \pi (a|s , \theta)\\ \\ \sum_a b(s) \bigtriangledown \pi (a|s , \theta) = b(s) \bigtriangledown \sum_a \pi (a|s , \theta) = b(s) \bigtriangledown 1 = 0 \]

实际上b(s)只要是与action无关的函数即可，甚至是随机数都可以。那为什么还要引入这个b(s)呢，因为b(s)不改变参数更新的期望（引入的更新变化期望为0），同时可以通过选择合适的b(s)降低模型方差(MC方法通常方差比较大)，通常的一个做法是把对v(s,w)的建模作为b(s)进行训练

Actor–Critic Methods

同时对policy和state-value建模，并应用于boostrapping方法（上面的REINFORCE baseline方法也同时对policy和state-value建模，但没有用于boostrapping）

联系我: