前端时间在读一本讲混沌理论的书《复杂》,发现里面有一个很有趣的方程\( x_{t+1} = Rx_t(1-x_t)\) 其中 \(x\in {0,1} \),这个方程形式虽然很简单,但是会有很多有趣的现象,我写了个简单的程序反映这个现象放在了Github上面,感兴趣可以下载下来玩玩。
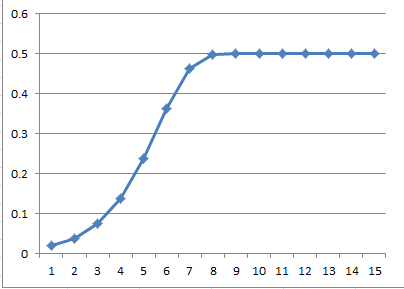
当\(R = 2\)时,\(x=0.01\)时

当\(R = 2\)时,\(x=0.8\)时
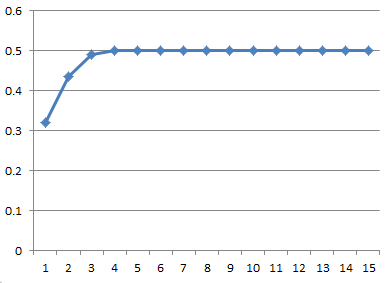
可以多尝试一些\(x\)的取值,会发现无论\(x\)的取值是多少,最后都会收敛到0.5。收敛到的值会随着\(R\)变化而变化,如果把\(R\)值换成2.5,最终收敛的值就变成了0.6。
并不是所有的\(R\)都会导致数列最终收敛到一个点上,比如\(R = 3.1\)时,系统不会收敛到一个固定点,而是最终在两个点上来回震荡,这种震荡现象同样也是对所有\(x\)都成立的。
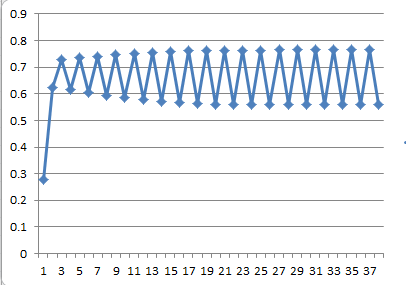
随着\(R\)的变化,一直到\(R = 0.34\),都会出现在两个点上震动的现象,系统的周期为2。
在\(R\)取值范围在0.34~0.35之间时,无论\(x\)取什么初值,系统最终都会在四个点上来回震动,系统周期变为了4。
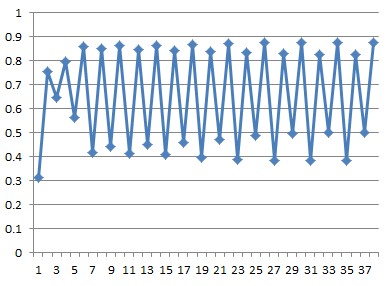
在3.54 和 3.55之间的某个\(R\)值, 周期再次突然倍增,一下跃升到8。在3.564和3.565之间的某个值周期跃升到16。在3.5687和3.5688之间周期又跃升到32。周期一次又一次倍增,前后间隔也越来越小,很快,在 \(R\)大约等于3.569946时,系统的周期已经趋于无穷了。
费根鲍姆常数
物理学家费根鲍用计算机计算出了倍增周期R值表:
\(R_1 \approx 3.0\)
\(R_2 \approx 3.44949\)
\(R_3 \approx 3.54409\)
\(R_4 \approx 3.564407\)
\(R_5 \approx 3.568759\)
\(R_6 \approx 3.569692\)
\(R_7 \approx 3.569891\)
\(R_8 \approx 3.569934\)
…
\(R_{\infty} \approx 3.569946\)
其中\(R_1\)表示\(21\)倍周期,\(R_n\)表示\(2n\)倍周期
注意到随着周期数的增加,周期之间的\(R\)值差距逐渐减小,新周期倍增比前面一个周期倍增比快大约4.6692016倍。4.6692016被成为费根鲍常数。
这还不是费根鲍常数神奇的唯一的地方,研究还发现所有的单峰映射(罗蒂斯特映射只是其中之一)都遵循这个规律。
在有稳定周期的罗蒂斯特映射里,系统对初值是不敏感的,无论初值取什么最终都会进入到稳定的周期中。当系统的周期趋向于无穷之后,系统变得对初值敏感,而且随着\(R\)从3.569946变大,系统对初值变得越来越敏感,比如下图\(R = 4, x_0=0.2\)和\(x_0=0. 2000000001\),初值只有微小的变化,两个数列会很快(约30次迭代之后)分开。
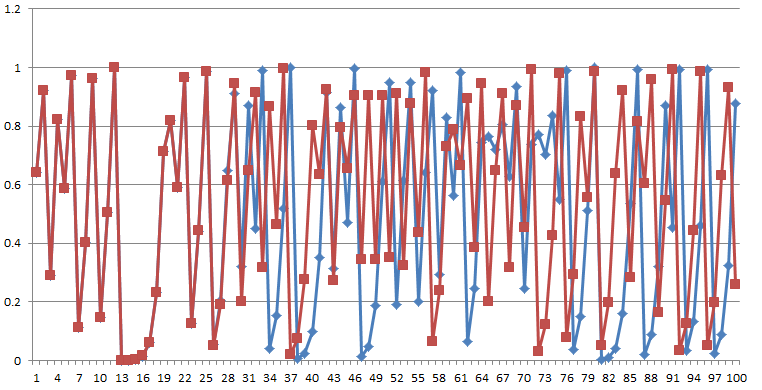
关于这个变化,维基百科上有更精确的描述:
0和1之间:不论启始值数值为何, \(x_{n}\)会越来越少,最后趋近于0。
1和2之间:不论启始值数值为何, \(x_{n}\)会快速的趋近 \({\frac{r-1}{r}}\)
2和3之间:经过几次迭代, \(x_{n}\)也会越来越接近\({\frac{r-1}{r}}\) ,但一开始会在这个值左右振动,而收敛速率是线性的。
3: \(x_{n}\) 仍然会越来越接近 \({\frac{r-1}{r}}\),但收敛速率极为缓慢,不是线性的。
3和\(1+\sqrt{6}\) 之间(约3.45)之间:针对几乎所有的初值, \( x_n \) 最后会在2个值之间持续的震荡,即 \(x_{n}\)最后会是a,b,a,b…的变化,其数值和 \(r\)有关。
3.45和大约3.54之间,针对几乎所有的初值, \(x_{n}\)最后会在4个值之间持续的震荡。
约大于3.54: \(x_n\)最后会在8个、16个、32个值……之间持续的震荡,至于 \(r\)何时会令 \(x_{n}\)的值由n个到2n个,则和费根鲍姆常数4.669…有关。
约为3.5699:这样的振动消失,整个系统开始在混沌的状态之中。针对几乎所有的初值,都不会出现固定周期的震荡,初值再微小的变化,随着时间都会使结果产生明显的差异,这就是典型混沌的特性。
大于3.5699:整个系统在混沌的状态之中。不过,当中有些特定的\(r\)值还是使系统变成非混沌,有周期性的结果,这些区间称为“稳定岛”。例如当\(r\)约大于3.82,会出现3个值的周期,再大一点出现6个值及12个值的周期。
当 \(r\)从大约3.5699到大约3.8284之间,系统混沌性质发展的现象有时会称为Pomeau–Manneville场景,其特征是周期性的震荡和非周期性的行为会穿插出现。此特征可以应用在半导体元件中。也有其他区域会使系统的周期为5个值,不管任意周期都存在某特定的\(r\),使周期为指定值。
大于4:针对几乎所有的初值,系统最后都会超过区间[0,1]并且发散。
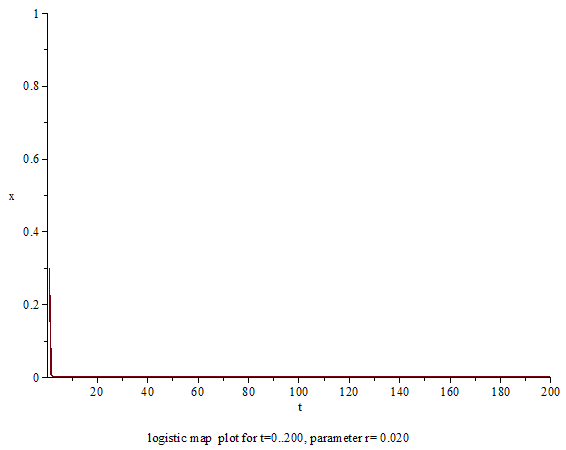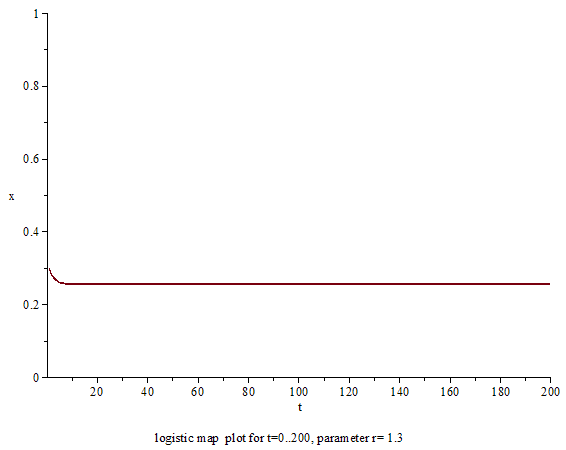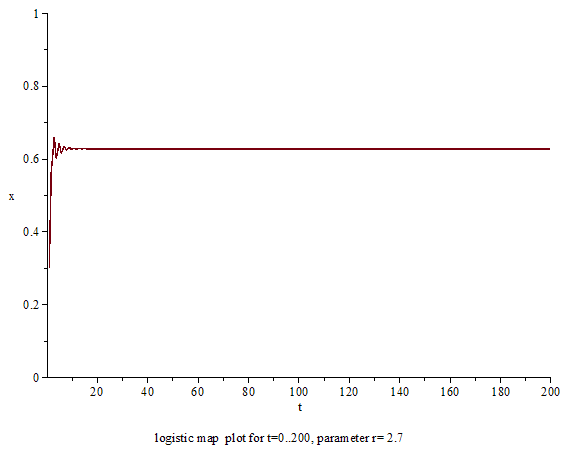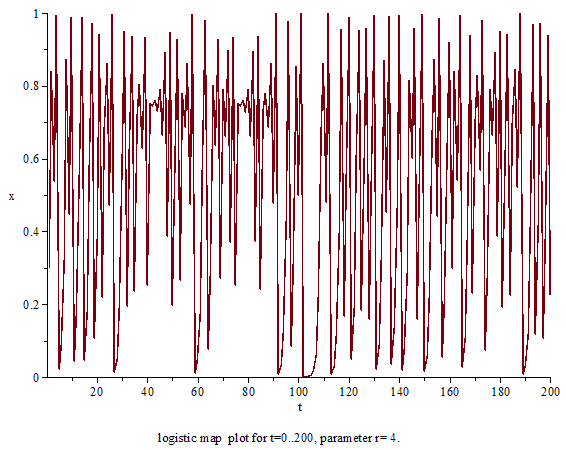
从罗蒂斯特映射可以看到即使是非常简单和确定的系统并不需要外界随机因素介入,也可能导致混沌现象,因为对初始条件的极端敏感,整个系统变得不可预测。这与人们常说的蝴蝶效应意思相同,事实上这个特性还可以用来生成计算机随机数,详见这里。
我这里还想简单聊一点混沌现象可以引发的一点哲学方面的思考,在牛顿的那个科学时代,人们普遍认为世界是决定性的,如果只要我们掌握了各种科学知识,只要知道了这个世界的全部初始条件,那么就可以把整个宇宙的从开始到结束全部推演出来,任何事件都是在预料之中的。所以人究竟有没有所谓的自由意志也是被质疑的,毕竟如果所有的事情都能够被预测,人的所作所为都被预测,那么人的所谓的自由意志似乎就是自欺欺人的玩笑,这就是所谓的决定论的思想。
决定论的思想听起来虽然有点吓人(否认了自由意志和全部事件可预测的推论让人觉得这个世界很乏味),但似乎从科学的原理上也说的过去。“如果只要我们掌握了各种科学知识,只要知道了这个世界的全部初始条件”,这个世界似乎还不想去掉最后这个神秘的面纱,随着量子力学的发展,人们发现了测不准原理,位置和动量不可同时被确定。这个测不准原理直接挑战了决定论的前提条件,人们不可能精确获得这个世界的全部初始条件,那么如果根据测不准原理,退而求其次只进行有限可信度的测量,能不能给予我们一个世界大概的演进推算,比如预言某件事有70%~80%的概率会发生呢,根据混沌的理论,初始值微小的变化也会导致结果的极大不同,因此结合测不准原理和混沌理论基本可以宣布先知式的决定论是不现实的,这个世界似乎又生动有趣了一点点:)
联系我