最近的工作中要借鉴到EM的思想把EM又重新整理了下总结此文
我们观察到的样本集有时候仅仅是最终反映出来结果即可观测的部分而内在的一些隐含的因素往往不能被直接观察到但算法不能忽略这些隐含状态建模时要包含这些隐状态而这样的模型有时候会比较复杂导致直接优化原目标函数不得不退而求其次利用琴生不等式的性质优化下确界这就是EM的初衷了
包含隐变量的loglikelihood的估计常常会用到EM这种情况下优化目标函数形式是
$$L = \sum_i {log{\sum_z {p(x,z;\theta)}}}$$
其中x表示观测到的样本集z表示隐变量\(\theta\) 代表模型参数注意到这个目标函数log里面包含求和符号\(\sum\)这会导致模型优化上的复杂性为了简化计算利用琴生不等式有
$$L = \sum_i {log{\sum_z {q(z) \frac{p(x,z;\theta)}{q(z)}}}}$$
$$ \quad \geqslant \sum_i \sum_z {q(z)} {log{ \frac{p(x,z;\theta)}{q(z)}}}$$
EM算法不再优化原目标函数而是优化更容易优化目标函数的下确界在优化下确界时分为E步和M步E步中计算目标函数对隐变量进行分析M步中利用E步对隐变量分析的结果重新评估模型参数来达到最大化目标函数的目的换句话说E步计算隐变量M步计算模型参数不停地重复E步和M步直到收敛
这里还有一个问题没有解决优化时引入了q(z)但q(z)的公式到底应该怎么表示呢注意到上述应用琴生不等式的步骤可以表述为
$$ log({E_z{[\frac{p(x,z;\theta)}{q(z)}]})} \geqslant E_z{[log({\frac{p(x,z;\theta)}{q(z)}})] } $$
上式如果等号成立必有 $$\frac{p(x,z;\theta)}{q(z)} = c $$
$$ s.t. \sum_z q(z) = 1 $$ 可以得到
$$ q(z) = \frac{p(x,z;\theta)}{\sum_z p(x,z;\theta)} $$
$$ \quad = \frac{p(x,z;\theta)}{p(x;\theta)} $$
$$ \quad = {p(z|x;\theta)} $$
参考文献1举了一个很好掷硬币例子可惜没有针对这个例子进行完整的理论分析也没有相应的代码提供这里我进行了一些完善希望可以更加容易的理解EM算法
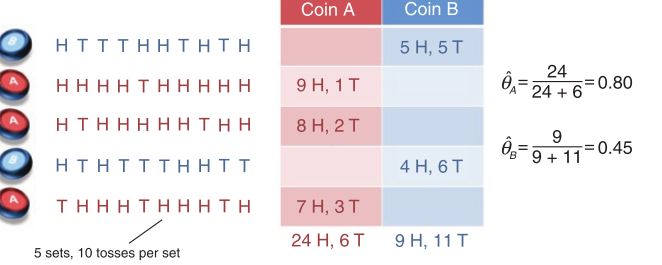
考虑两个非标准的硬币这里的非标准是指掷硬币时正反面概率不是相等的对这两个硬币共进行了5组实验每组实验开始前先选定一个硬币然后用这个选定的硬币进行十次投掷对结果进行记录如下图所示

可以看到第一组四组使用了硬币B第二三五组使用硬币A使用最大似然估计这两个硬币扔出正面的概率A硬币共进行3组实验共投掷30次其中24次正面所以投掷正面的概率为0.8B硬币共进行了两组实验共投掷20次其中9次正面所以投掷正面的概率为0.45
上面的小例子应该是大部分人学习概率的第一个例子下面对这个小例子进行一点点小小的变化引入EM算法中重要的概念—–隐变量仍然是上面的五组实验数据现在假设不知道每组实验是由哪个硬币投掷的只观测到每次投掷的正反面如何利用最大似然求每个硬币投掷时正面朝上的概率呢
在新的状况下我们只观测到了一部分数据即只有每次投掷结果是正面还是反面被观察到另外一部分数据没有被观察到即每组实验是采用的哪个硬币这里可以发现现在的情况和EM算法提出的动机一样了所以也就意味着可以用EM算法来解决这个问题为了使用EM算法来解决问题首先引入一些变量
\(i \in { 1,2,3,4,5 }\)表示第i组实验
\(h_i\) 表示第i组实验中正面朝上的次数
\(n_i\) 表示第i组试验中反面朝上的次数
x_i 表示第i组实验的观测结果
z_i 表示第i组实验是有硬币\(z_i\)掷出的
\({p_A}^{(t)}\) 表示第t轮迭代A硬币正面朝上的概率
\({p_B}^{(t)}\) 表示第t轮迭代B硬币正面朝上的概率
有了这些变量按照EM算法的流程首先随机初始化\({p_A}^{t=0}\)和\({p_A}^{t=0}\)然后E步M步交替执行知道收敛
第t轮E步
\(\quad\quad\quad\quad\)计算loglikelihood L并对隐变量进行分析
$$q^{(t)}(z_i=A) = \frac{p(x_i,z_i=A)}{\sum_{z_i} p(x_i,z_i)} = \frac{{p_A^{(t-1)}}^{h_i}{(1 - p_A^{(t-1)})}^{n_i}}{{p_A^{(t-1)}}^{h_i}{(1 - p_A^{(t-1)})}^{n_i} + {p_B^{(t-1)}}^{h_i}{(1 - p_B^{(t-1)})}^{n_i}}$$
$$q^{(t)}(z_i=B) = \frac{p(x_i,z_i=B)}{\sum_{z_i} p(x_i,z_i)} = \frac{{p_B^{(t-1)}}^{h_i}{(1 - p_B^{(t-1)})}^{n_i}}{{p_A^{(t-1)}}^{h_i}{(1 - p_A^{(t-1)})}^{n_i} + {p_B^{(t-1)}}^{h_i}{(1 - p_B^{(t-1)})}^{n_i}}$$
第t轮E步
\(\quad\quad\quad\quad\)最大化loglikelihood L求得使L最大化的\({P_A}^{(t)}\)和\({P_B}^{(t)}\)供下轮迭代使用
$$L = \sum_i log(\sum_z p(x_i,z_i))$$
$$\quad = \sum_i log(\sum_z q(z)\frac{p(x_i,z_i)}{q(z)})$$
$$\quad \geqslant \sum_i \sum_z q(z) log(\frac{p(x_i,z_i)}{q(z)})$$
$$\quad \quad\quad \quad\quad \quad\quad \quad\quad \quad \quad \quad\quad \quad\quad \quad\quad = \sum_i { q(z_i=A) log(\frac{p(x_i,z_i=A)}{q(z_i=A)}) + q(z_i=B) log(\frac{p(x_i,z_i=B)}{q(z_i=B)}) }$$
$$ \quad \quad\quad \quad\quad \quad\quad \quad\quad \quad \quad \quad\quad \quad\quad \quad\quad = \sum_i { q(z_i=A) log(\frac{{p_A}^{h_i}{(1-p_A)}^{n_i}}{q(z_i=A)}) + q(z_i=B) log(\frac{{p_B}^{h_i}{(1-p_B)}^{n_i}}{q(z_i=B)}) } $$
$$\quad \quad\quad \quad\quad \quad\quad \quad\quad \quad \quad \quad\quad \quad\quad \quad\quad = \sum_i { q(z_i=A)[ h_ilog(p_A) + n_i log(1-p_A)] + q(z_i=B)[ h_ilog(p_B) + n_i log(1-p_B)] + C }$$
其中\(q(z_i=A)\)和\(q(z_i=B)\)已经在E步求得所以是常数
为求使得L最大的\(p_A\)和\(p_B\)有
$$ \frac{\partial L}{\partial p_A} = \sum_i \frac{q(z_i = A)h_i}{p_A} - \frac{q(z_i = A)n_i}{1-p_A} = 0 $$
$$ \sum_i {q(z_i = A) h_i (1-p_A)} - {q(z_i = A)n_ip_A} = 0 $$
$$p_A = \frac{\sum_i q(z_i=A)h_i}{\sum_i q(z_i=A)h_i + q(z_i=A)n_i} $$
同理
$$p_B = \frac{\sum_i q(z_i=B)h_i}{\sum_i q(z_i=B)h_i + q(z_i=B)n_i}$$
整个迭代过程如下图所示
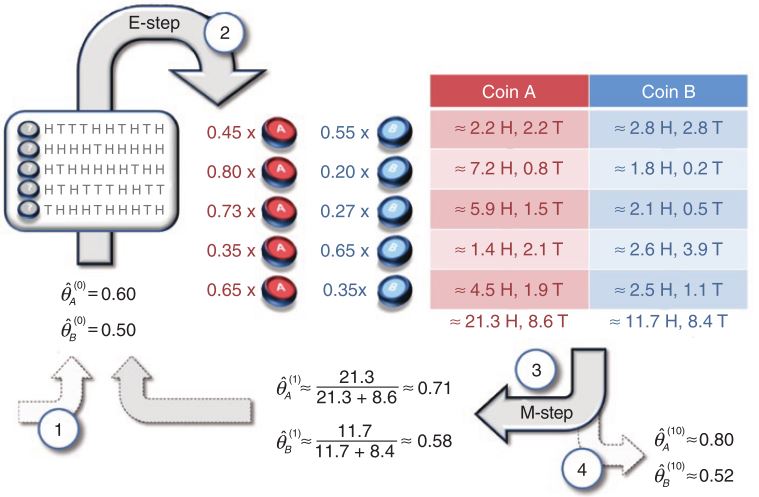
想查看这个代码可以从这里下载迭代结果如下
[epoch 0] pa=0.600000 pb=0.500000
[epoch 1] pa=0.713012 pb=0.581339
[epoch 2] pa=0.745292 pb=0.569256
[epoch 3] pa=0.768099 pb=0.549536
[epoch 4] pa=0.783165 pb=0.534617
[epoch 5] pa=0.791055 pb=0.526281
[epoch 6] pa=0.794532 pb=0.522390
[epoch 7] pa=0.795929 pb=0.520730
[epoch 8] pa=0.796466 pb=0.520047
[epoch 9] pa=0.796668 pb=0.519770
[epoch 10] pa=0.796744 pb=0.519659
ealy stop delta1=0.000028 delta2=0.000045
1What is the expectation maximization algorithm? Chuong B Do & Serafim Batzoglou
2The Expectation Maximization Algorithm frank dellaert
3CS229 Lecture notes-8 The EM algorithm Andrew Ng
联系我