正则化是机器学习方法实践中用于避免overfitting的主要方法,给优化目标加上基于L1、L2的正则项是常用的正则化方法。之前自己在实现一些机器学习方法时一直是使用L2的方法,因为L2正则项有连续可微的性质,在求导时特别方便,而基于L1的正则项(lasso)并不是处处连续的,因此在优化时有一定的难度。
虽然L1解起来有一定的难度,但是它的好处也比较明显,L1能够产生稀疏解(sparsity),而通常稀疏解的泛化能力会比较好,之前也听说过Proximal Algorithm是求解L1的很好的方法,粗看了一次也没能搞懂,后面就偷懒一直没有去学习这个方法,前段时间有机会参加CCF-ADL70的学习班,听了James Kwok的报告,讲的非常清楚,收获颇丰,Proximal Algorithm方法也在报告的内容之中,查阅一些文献总结一些粗浅认识,成了此文。
为了追求更好的模型效果,往往使用更复杂的模型,模型的维度都是非常大的,非常容易造成过拟合(overfitting)的现象,实践中发现使用L1可以产生稀疏解,而稀疏解的模型不容易过拟合,泛化能力更好。
那么为什么使用L1就可以产生稀疏的解,而使用L2就不会呢,可以看下面一个小例子:
$$ min_{z \in R\quad}{L = \lambda|z| + \frac{\gamma}{2} {(z - x)}^2} $$
当\(z>0\)时有:
$$\frac{\partial L}{\partial z} = \lambda + \gamma(z - x) = 0$$
$$ z = x - \frac{\lambda}{\gamma} \quad\quad (z > 0)$$
当\(z<0\)时有:
$$\frac{\partial L}{\partial z} = -\lambda + \gamma(z - x)$$
$$z = x + \frac{\lambda}{\gamma} \quad\quad (z < 0)$$
综上,当\(x> \frac{\lambda}{\gamma}\)时,\(z = x - \frac{\lambda}{\gamma}\);当\(x < -\frac{\lambda}{\gamma}\)时,\(z = x + \frac{\lambda}{\gamma}\);当\(-\frac{\lambda}{\gamma} <= x <= \frac{\lambda}{\gamma}\)时,\(z=0\),可见L1容易产生稀疏解。
那么,如果这里的优化目标不采用L1的正则项,而是采用L2正则项会怎么样呢?
$$ min_{z \in R\quad}{L = \frac{1}{2}\lambda {z}^2 + \frac{\gamma}{2} {(z - x)}^2} $$
可直接求导: $$\frac{\partial L}{\partial z} = \lambda z + \gamma(z-x) = 0$$
$$ z = \frac{\gamma}{\lambda + \gamma} x $$
可见L2的正则项,即使x是很接近0的数,z也只是变成了比x更接近0而已,并不能变成0,而L1的正则项可以得到0。
对于目标函数不是处处连续可微的情况,通常是使用次梯度(subgradient)来进行优化,由于次梯度自身的原因会导致两方面问题:
Proximal Algorithm 自然肩负了要解决这两个问题的使命。
是时候揭开Proximal Algorithm的什么面纱了,首先先定义算法的核心部分proximal operator:
$$prox_{\lambda f}(v) = argmin_x {(f(x) + \frac{1}{2\lambda}{||x - v ||}^2)}$$
从上面这个式子可以看出,上式是在寻找一个距离v点不要太远的一个x,使得f(x)尽可能小,显然\(f(x) <= f(v)\)。

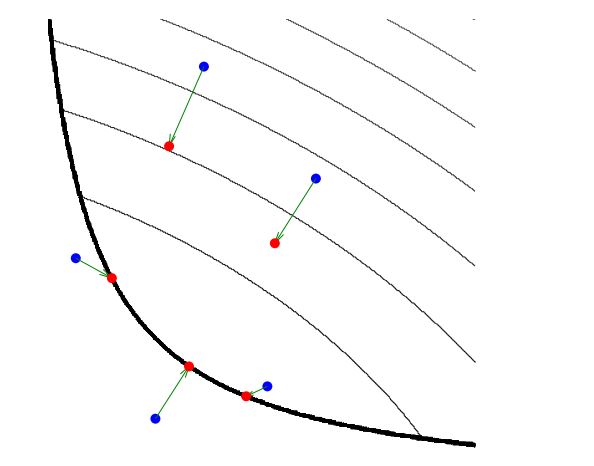
图片来自《Proximal Algorithms in Statistics and Machine Learning》2,这张图形象的表示了上面式子的几何意义,其中加粗的黑线表示作用域,浅色的黑线表示函数f的等高线,蓝色的点对应上面式子的v点,红色点表示最终求得的x点。
接下来介绍使用Proximal Gradient Method优化,上面提到的prox式子仿佛在优化算法里常用的迭代优化的步骤,从v点出发,找到一个更好的点x,使得\(f(x) <= f(v)\)。
设待优化目标函数为\(F(x) = l(x) + \phi(x)\),其中\(l(x)\)是连续可微的,\(\phi(x)\)不是处处连续的,这类优化目标在机器学习中比较常见,如\(l(x)\)表示最小二乘的拟合误差,\(\phi(x)\)表示L1正则化因子用于产生稀疏解。
Proximal Gradient Algorithm
for t = 1,2…n
1) Gradient Step,定义\({v}^t\)是沿着\(l(x)\)梯度方向找到的一个点:
$${v}^t = {x}^t - \gamma\bigtriangledown l({x}^t)$$
2) Proximal Operator Step,使用prox式子优化\(phi(x)\)
$${x}^{t+1} = prox_{\lambda \phi} ({v}^t) $$
直到收敛或达到最大迭代次数
这里有一个没有提到的是参数\(\lambda\)的选择,proximal算法中要求\(\bigtriangledown l(x)\)满足Lipschitz continuity 系数为L,那么只需让\(\lambda \in (0, \frac{1}{L})\) 即可,若L的取值未知,可以使用line search的方法去找:
repeat
\(z = prox_{\lambda \phi} ({v}^t)\)
break if \(f(z) <= f({v}^t) + \bigtriangledown {f}^T({v}^t)({v}^2 - z) + \frac{1}{2\lambda}{||{v}^t - z||}^2 \)
\(\lambda = \frac{1}{2}\lambda\)
return \({x}^{t+1} = z\)
可能会有人和我一样觉得上面算法第二步直接应用proximal operator觉得有些生硬,通常情况下大家已经习惯使用Stochastic Gradient Descent(sgd)直接优化满足处处可微的目标函数,这二者之间有哪些关系呢?
SGD是把目标函数进行一阶泰勒展开,Proximal Algorithm也是同样的,只不过Proximal Aglorithm更为严格,要求目标函数\(F(x) = l(x) + \phi(x)\),其中\(\bigtriangledown l(x)\)满足Lipschitz continuity,有:
$$ F(x) = l(x) + \phi(x) \leqslant l(x_0) + {(x-x_0)}^{T}\bigtriangledown l(x_0) + \frac{1}{2\gamma}{||x-x_0||}^{2} + \phi(x) $$
$$ where \quad \gamma \in (0, \frac{1}{L}] $$
寻找可以使F(x)最小化的x,因为直接求解F(x)不容易求解,所以转为求使得F(x)上确界的最小的x,即
$$ x = argmin_{x}{{l(x_0) + {(x-x_0)}^{T}\bigtriangledown l(x_0) + \frac{1}{2\gamma}{||x-x_0||}^{2} + \phi(x)}} $$
凑方并增减常数项,得:
$$x = argmin_x {(f(x) + \frac{1}{2\lambda}{||x - u ||}^2)}$$
$$ where\quad u= x_0 - \gamma\bigtriangledown l(x_0)$$
由此可见,Proximal Aglorithm是在目标函数F不满足处处可微条件时,可以转而去优化目标函数的上界的自然结果。
最小化目标函数的优化方法中,SGD的思路是,先找到目标函数的梯度方向,然后沿着梯度方向去寻找一个步长,使得在新的坐标点上目标函数值降低。除了SGD,还有一种做最优化的基本方法,是Trust Region方法,因为在实战中泰勒公式通常只展开到一阶或二阶,高阶项被丢弃,要使得被丢弃的高阶项不至于对优化造成太大影响,下一个坐标点必须不能离原坐标点距离太大,因此Trust Region先在当前坐标点附近寻找一个小的信赖区域(类比SGD中的步长),然后在这个区域内寻找使目标函数最小的坐标点。
$$prox_{\lambda f}(v) = argmin_x {(f(x) + \frac{1}{2\lambda}{||x - v ||}^2)}$$
Proximal Algorithm的式子里也体现着这种思想,最小化f(x)且要求新求得的x点不能和上一轮迭代得到的v点距离太远。
最后这两个话题超过这篇小文想要介绍的范围了,以后或许会再写文章介绍这两个话题,这里只提一下。
有不少研究是想让Proximal Algorithm更快,提高收敛速度,最简单的引入神经网络中常用的“冲量”即可以加速这个算法,其他更多改进算法需要去查阅更多资料了(PS,张潼老师也做相关研究)。
使用Proximal Algorithm 求解一些lasso的问题的根本原因是Proximal Algorithm用起来很方便,求解很快。但Proximal Algorithm也不是对所有问题都是很方便的,比如它对L1这种,\(\phi(x) = \sum |x_i| \) non-overlapping的很容易求解,对于一些其他的正则项如Group lasso就没有这么方便求解了,因此又提出了Alternating Direction Method of Multipliers(ADMM)算法用来求解这种问题。
1 《Big Machine Learning》 James Kwok, CCF ADL70
2 《Proximal Algorithms in Statistics and Machine Learning》 Nicholas G. Polson, James G. Scott, Brandon T. Willard
3 《Proximal Algorithms》 Neal Parikh,Stephen Boyd
联系我: