实际的生产生活中很多问题被建模为线性规划问题进行求解,所谓线性规划问题,即目标函数和约束条件都是线性的,形式化的表示为:
$$ min \quad c^{T}x $$
$$ s.t. Ax=b $$
$$ x >= 0 $$
其中A为m行n列的矩阵,n和变量个数相等,可行域线性约束\( Ax=b \) 可能无界、唯一解、无穷多解三种可能,其中前两种对于优化问题来说没有意义,只研究有无穷多解的情况,不妨设A矩阵为行满秩的,因为有无穷多解,必有\( m < n\)。
多面体是集合空间中的多个半平面的交集,表示为\( S = \{x| Ax <=b \}\),这种表示方法比较容易理解。
这种表示法与上述线性规划的可行域\( \{x| Ax = b, x >= 0 \}\)是等价的,首先可以假设所有的x满足\(x>=0\),因为若存在:
$$ kx <= b $$
$$ \Rightarrow x <= \frac{b}{k}$$
$$ \Rightarrow x - \frac{b}{k} <= 0 $$
$$ \Rightarrow x' = \frac{b}{k} -x >= 0 $$
其次,对于:
$$ Ax <= b;\quad\quad x>=0 $$
$$ \Rightarrow Ax + z = b;\quad\quad x,z>=0$$
$$ \Rightarrow (A,1)(x,z) = b;\quad\quad x,z>=0$$
$$ \Rightarrow A'x' = b;\quad\quad x'>=0 $$
综上,两种表示方法\( \{x| Ax <=b \}\)和\( \{x| Ax = b, x >= 0 \}\)是等价的。

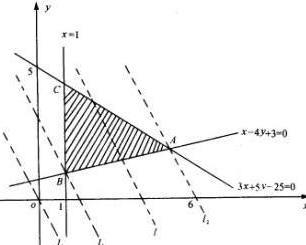
图片来自这里。目标函数是线性函数,可行域为多面体,如上图,极值一定在多面体的定点处得到。
前面提到A是m行n列的矩阵,m < n,且是行满秩的,可以表示为A=(B,N),其中B是可逆矩阵。同样的拆分x为 xT = (\(x_B,x_N\))。Ax = \(Bx_B+Nx_N\) = b,令\(x_N\) =0,有xB = \(B^{−1}b\),称xT = \((B^{−1}b,0)\)为基本解,\(x_B\)为基变量,\(x_N\)为非基变量,若\(B^{−1}b\)>0,xT = \((B^{−1}b,0)\)为基本可行解。注意基本可行解和多面体的顶点一一对应。
多面体两个相邻的顶点,有且只有一个基变量不同。
综上,线性规划的极值一定在顶点处取得,且顶点和基本可行解一一对应,那么因为多面体的顶点数是有限的,穷举所有基本可行解即可得到线性规划问题的极值。
这种方法的复杂度为O(\(C_{n}^{m}\) m3) = O(nm m3),这种方法复杂度很高,需要寻找一种更加高效的方法。
单纯形法的求解思路源自上述求解线性规划的朴素想法,主要思路是既然穷举所有基本可行解的代价比较高,那么需要设计一种聪明的方法来避免穷举,单纯形法给出的方案是从一个初始的多面体的顶点出发,找到一个比当前定点让目标函数更小的邻接顶点,在更新的顶点上继续寻找能够让目标函数更小的邻接顶点,依次类推,直到找不到一个邻接顶点比当前点更小。
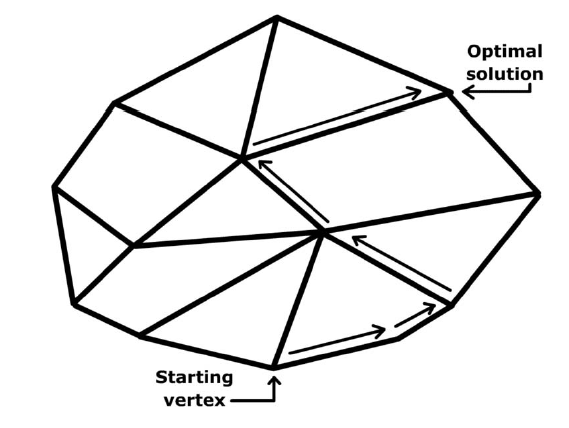
( 图片来自孙小玲老师的讲义)
要找到线性规划的最优解,首先需要能够识别最优解,即算法在什么时候停止。设\(\widehat{x}\)T = \((B^{-1}b,0)\) 为当前的基本可行解。对于可行域上的任意xT = \((x_B, x_N)\),cT = \((c_B, c_N)\),有:
$$ c^T x = c^T_B x_B + c^T_N x_N $$ $$ = c^T_B B^{-1}b - c^T_B B^{-1}N x_N + c^T_N x_N$$
$$ = c^T \widehat{x} + (c^T_N - c^T_BB^{-1}N)x_N$$
令\(r_N = c^T_N - c^T_BB^{-1}N \),\(r_N\)被称为reduce cost,如果\(r_N\)>0,则当前的\(\widehat{x}\)为最优解。反之,说明当前解非最优解,假设\(r_j\) < 0,那么第j个非基变量加入基本可行解中(进基),同时需要选一个原来在基本可行解中的基变量令其等于零(出基),新的顶点目标函数已经比之前的小,因为多面体顶点数是有穷个,且目标函数在迭代过程中一直在朝目标值变小的方向,因此算法一定可以收敛。
单纯形法步骤:
步骤1:计算一个基本可行解xT = \((B^{-1}b,0)\)
步骤2:如果\(r_N = c^T_N - c^T_BB^{-1}N \) >0,计算停止,当前解为最优解,否则继续进行计算
步骤3:选择一个j,有\(r_j = c_j - c^T_BB^{-1}a_j \) < 0,(其中\(a_j\)表示N的第j行)。如果\(\overline{a_j} = B^{-1}a_j\) < 0,则目标函数无界,否则选择\(x_j\)入基
步骤4:计算 $$ \lambda = min \{\frac{\overline{b_i}}{\overline{a_{ij}} } | \overline{a_{ij}} >0 \} = \frac{b_r}{a_{rj}} $$
令\(x_j\ = \lambda\), x_r = 0。
在计算单纯形法时,单纯性表是一个很有用的辅助工具:
| \(x_B\) | \(x_N\) | rhs |
|---|---|---|
| B | N | b |
| \(c^T_B\) | \(c^T_N\) | 0 |
经过行列式变换得:
| \(x_B\) | \(x_N\) | rhs |
|---|---|---|
| I | \(B^{-1}N\) | b |
| 0 | \(c^T_N - c^T_BB^{-1}N\) | \(- c^T_BB^{-1}b\) |
最后留一道线性规划题目,要求使用单纯形法来求解:)
$$ min -7x_1 - 2x_2$$
$$ s.t. -x_1 + 2x_2 + x_3 = 4;$$ $$ 5x_1 + x_2 + x_4 = 20;$$ $$ 2x_1 + 2x_2 - x_5 = 7;$$ $$ x >= 0 $$
答案:最优解的目标函数值是\(-30\frac{2}{11}\)
1)孙小玲 《整数规划》
2)孙小玲 国立台湾大学课程及讲义
联系我: